Parabola In Standard Form - Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. Its general equation is of the form. Definition a parabola is a curve where any point is at an equal distance from: The parabola is a member of the family of conic sections. A fixed point (the focus), and a fixed straight line (the directrix) A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an.
Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. The parabola is a member of the family of conic sections. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Definition a parabola is a curve where any point is at an equal distance from: Its general equation is of the form. A fixed point (the focus), and a fixed straight line (the directrix)
The parabola is a member of the family of conic sections. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. A fixed point (the focus), and a fixed straight line (the directrix) Definition a parabola is a curve where any point is at an equal distance from: Its general equation is of the form. Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an.
Parabola Equation Properties Examples Parabola Formul vrogue.co
Its general equation is of the form. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. Definition a parabola is a curve where any point is at an equal distance from: The parabola is an open curve that is a conic section produced.
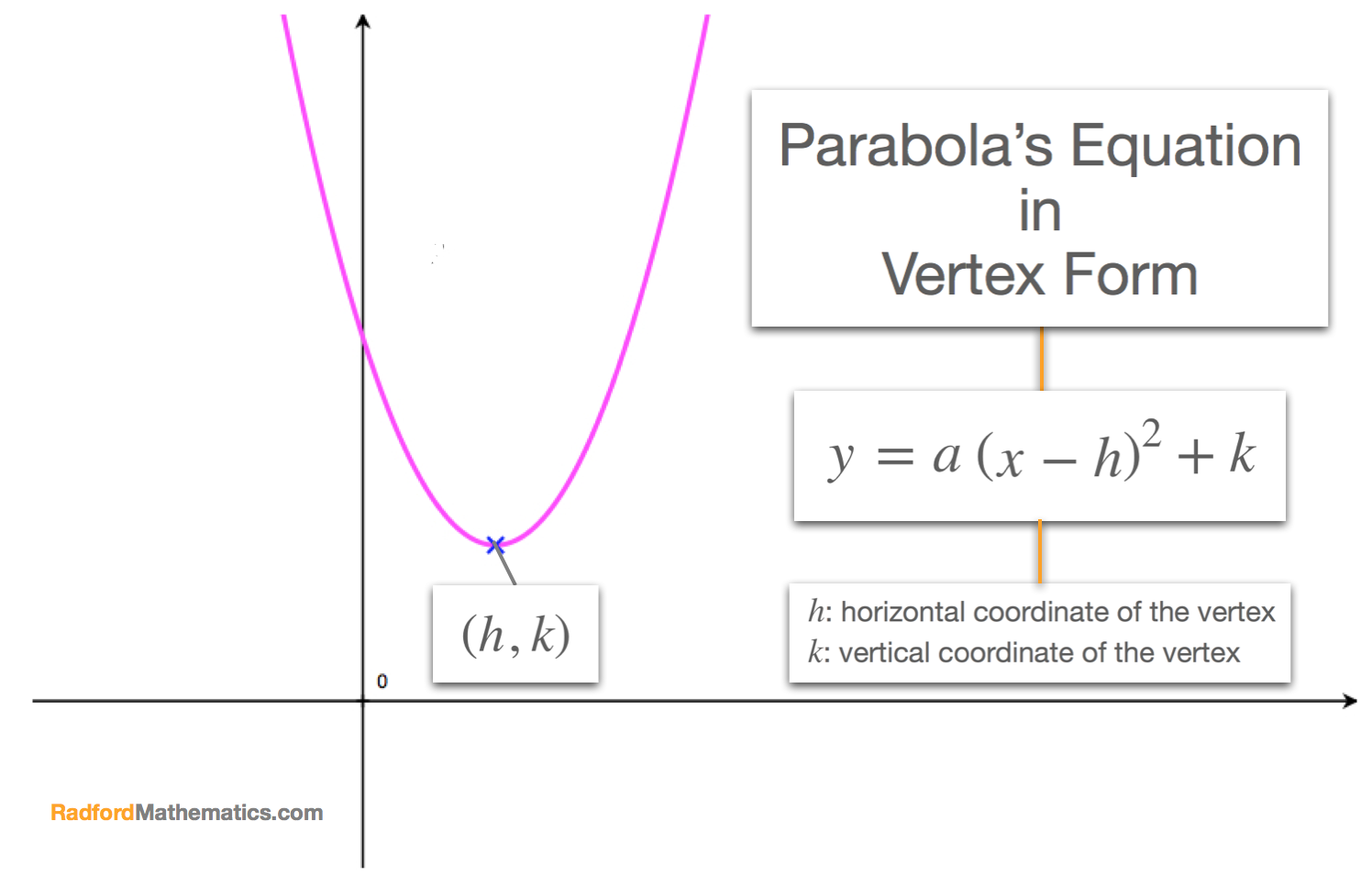
Parabola Equation Standard Form
A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. Definition a parabola is a curve where any.
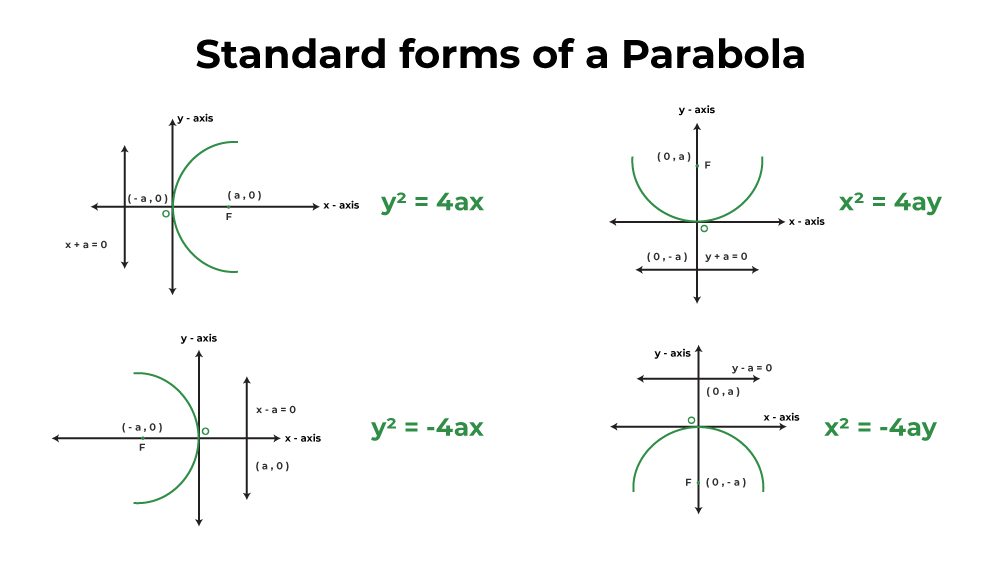
Standard Form Of A Parabola
Definition a parabola is a curve where any point is at an equal distance from: The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. The parabola is a member of the family of conic sections. Definition and key elements a parabola is a.
Properties And Equations For Parabolas
Definition a parabola is a curve where any point is at an equal distance from: Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. The parabola is an open curve that is a conic section produced by the intersection of a right circular.
Parabola Equation Standard Form
Its general equation is of the form. Definition a parabola is a curve where any point is at an equal distance from: The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. A parabola refers to an equation of a curve, such that a.
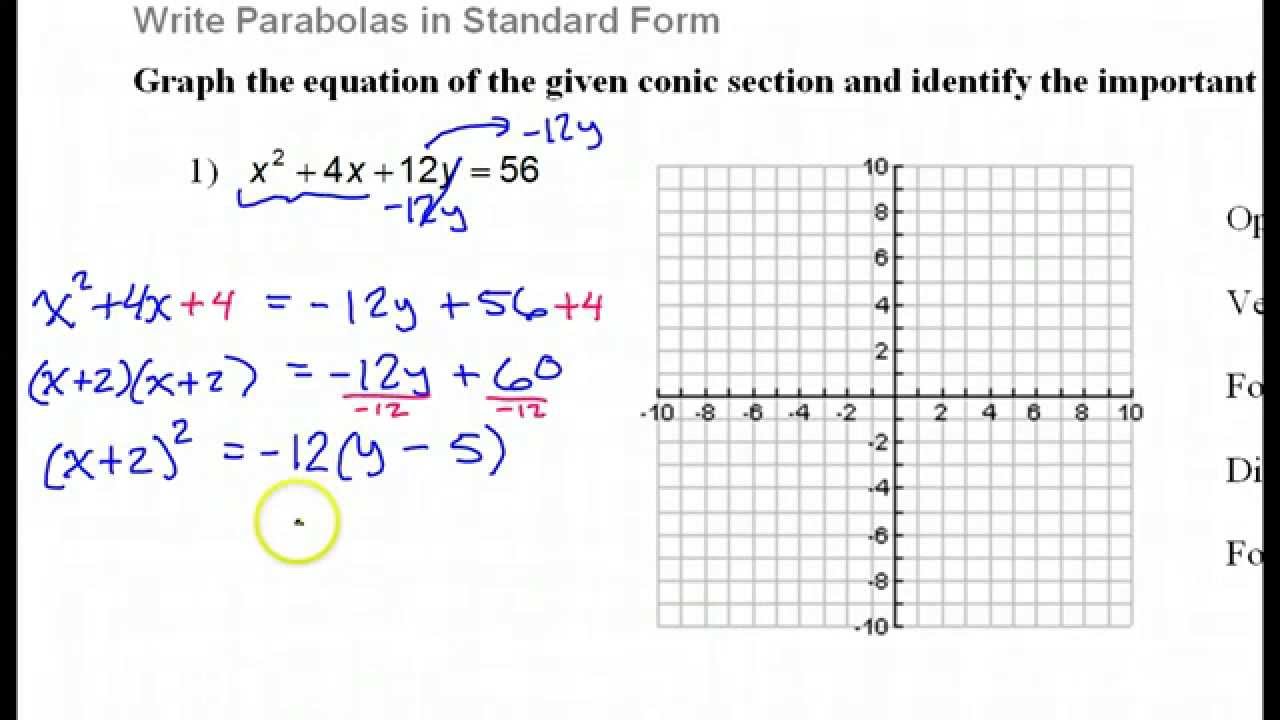
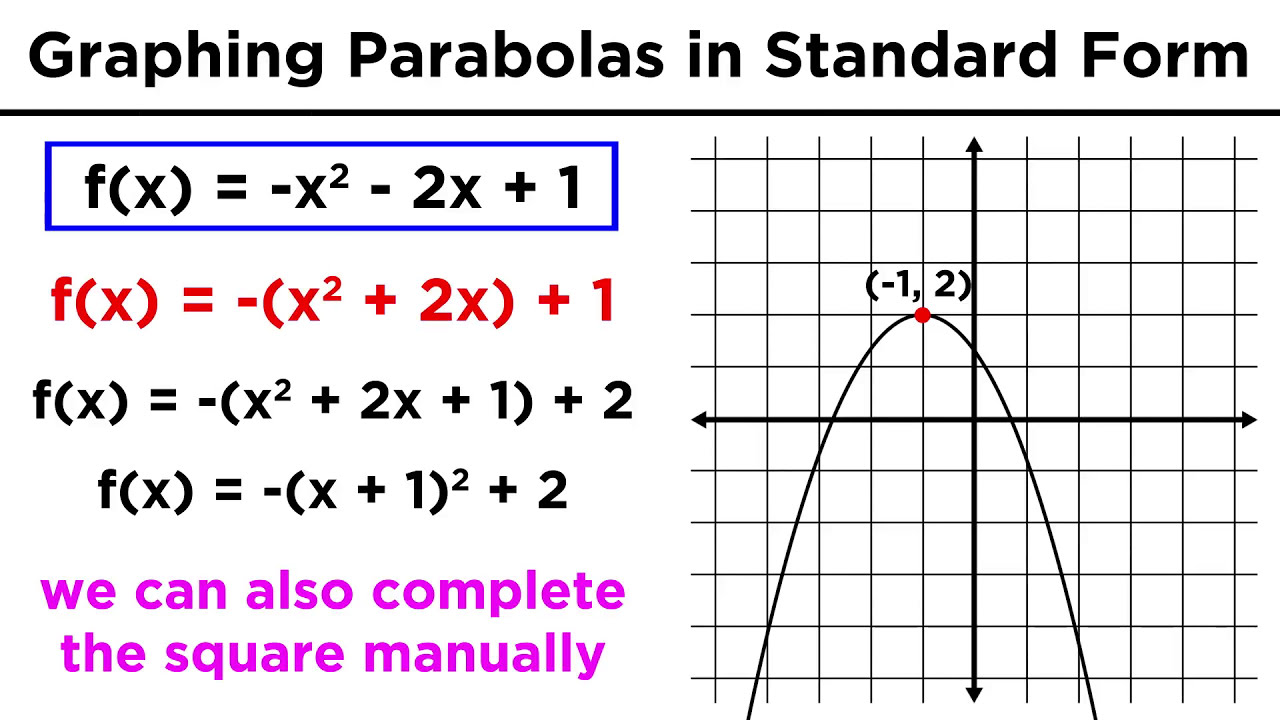
Write the quadratic equation in standard form for the parabola shown
Its general equation is of the form. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Definition a parabola is a curve where any point is at an equal distance from: A parabola refers to an equation of a curve, such that a.
Standard Form Equation For Parabola Calculator at Jeremy Burris blog
The parabola is a member of the family of conic sections. Its general equation is of the form. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. A fixed point (the focus), and a fixed straight line (the directrix) Definition a parabola is.
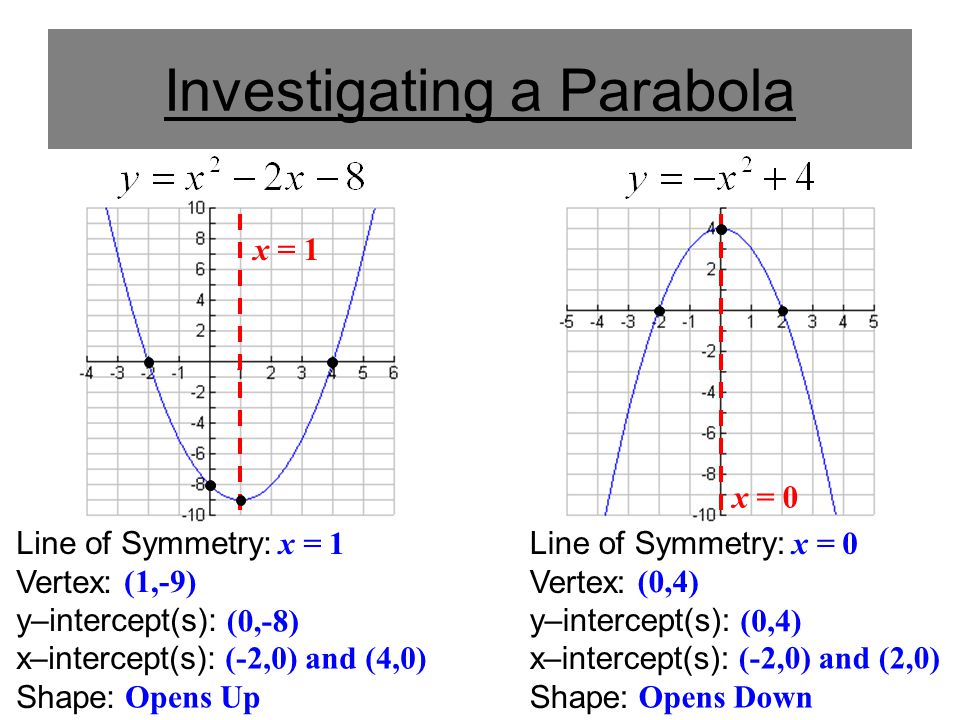
Parabola Graph, Properties, Examples & Equation of Parabola
Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. The parabola is an open curve that is.
Standard Form Equations, Examples Standard Form in Math
Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. Its general equation is of the form. A.
Graphing Conic Sections Part 3 Parabolas in Standard Form standard
The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A fixed point (the focus), and a fixed.
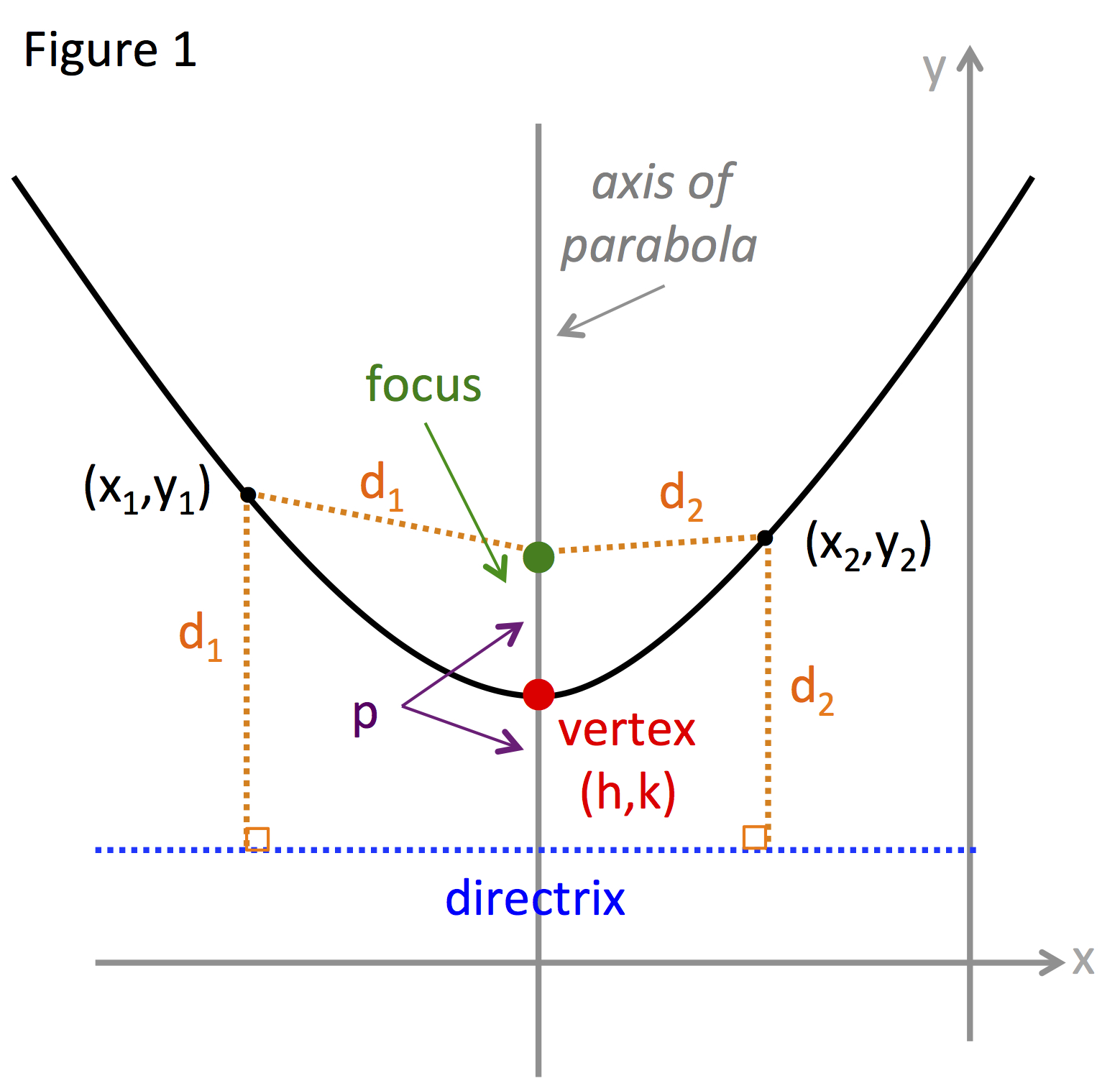
Definition A Parabola Is A Curve Where Any Point Is At An Equal Distance From:
A fixed point (the focus), and a fixed straight line (the directrix) The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. The parabola is a member of the family of conic sections. Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point.
A Parabola Refers To An Equation Of A Curve, Such That A Point On The Curve Is Equidistant From A Fixed Point And A Fixed Line.
Its general equation is of the form.