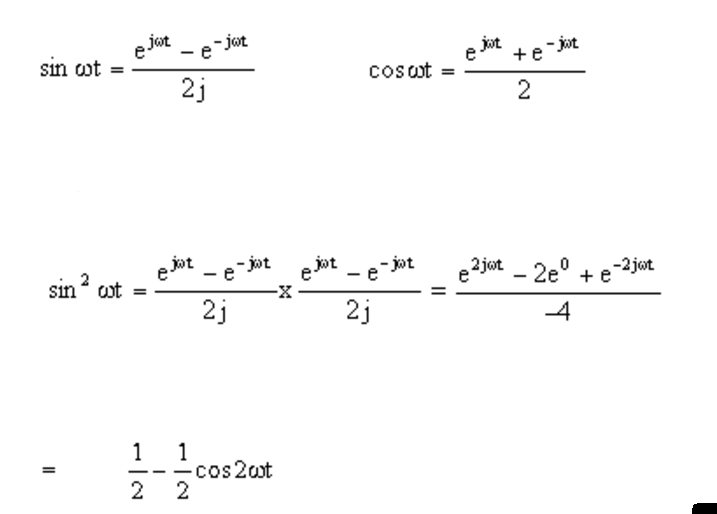
Sin Exponential Form - Euler’s formula can be established in at least three ways. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. Relations between cosine, sine and exponential functions. The functions of the form eat cos bt and eat sin bt come up in applications often. The first derivation is based on power series, where the exponential, sine and. To find their derivatives, we can either use the product rule or. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. From these relations and the properties of exponential multiplication you can painlessly.
To find their derivatives, we can either use the product rule or. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. From these relations and the properties of exponential multiplication you can painlessly. Euler’s formula can be established in at least three ways. The first derivation is based on power series, where the exponential, sine and. The functions of the form eat cos bt and eat sin bt come up in applications often. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. Relations between cosine, sine and exponential functions.
To find their derivatives, we can either use the product rule or. From these relations and the properties of exponential multiplication you can painlessly. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. Euler’s formula can be established in at least three ways. Relations between cosine, sine and exponential functions. The functions of the form eat cos bt and eat sin bt come up in applications often. The first derivation is based on power series, where the exponential, sine and. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,.
exercise 1 use eulers formula to prove the following formulas for cos x
From these relations and the properties of exponential multiplication you can painlessly. The first derivation is based on power series, where the exponential, sine and. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. Note that this technique.
Lesson Euler’s Formula for Trigonometric Identities Nagwa
Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. From these relations and the properties of exponential multiplication you can painlessly. Relations between cosine, sine and exponential functions. The functions of the form eat cos bt and eat.
Solved 23. (a) Use the complex exponential form of the
Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. From these relations and the properties of exponential multiplication you can painlessly. Euler's formula states that, for any real number x, one has where e is the base of the natural.
Sin and Cos Functions as Sums and Difference of Complex Exponential
Relations between cosine, sine and exponential functions. Euler’s formula can be established in at least three ways. To find their derivatives, we can either use the product rule or. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the..
QPSK modulation and generating signals
Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. To find their derivatives, we can either use the product rule or. Relations between cosine, sine and exponential functions. Euler’s formula can be established in at least three ways. From these.
Writing complex numbers in exponential form.using eulerdefinition for
The first derivation is based on power series, where the exponential, sine and. Euler’s formula can be established in at least three ways. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. From these relations and the properties.
Solved 1 z=8(cos i sin) in Exponential Form is out of O a.
To find their derivatives, we can either use the product rule or. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. The first derivation is based on power series, where the exponential, sine and. From these relations and the properties.
Solved THE EXPONENTIAL FORMS OF SIN AND COS Euler's formula
Relations between cosine, sine and exponential functions. To find their derivatives, we can either use the product rule or. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the. Note that this technique will typically give answers in a.
Other Math Archive January 29, 2018
The first derivation is based on power series, where the exponential, sine and. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. Euler’s formula can be established in at least three ways. Euler's formula states that, for any real number.
Writing complex numbers in exponential form using euler definition for
Relations between cosine, sine and exponential functions. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary.
To Find Their Derivatives, We Can Either Use The Product Rule Or.
Euler’s formula can be established in at least three ways. Note that this technique will typically give answers in a di erent form than the technique used in the book, giving not powers of the cosine or the sine,. The first derivation is based on power series, where the exponential, sine and. Relations between cosine, sine and exponential functions.
Euler's Formula States That, For Any Real Number X, One Has Where E Is The Base Of The Natural Logarithm, I Is The Imaginary Unit, And Cos And Sin Are The.
The functions of the form eat cos bt and eat sin bt come up in applications often. From these relations and the properties of exponential multiplication you can painlessly.